熱膨張率

熱膨張率（ねつぼうちょうりつ、英: coefficient of thermal expansion、略: CTE）は、温度の上昇によって物体の長さ・体積が膨張（熱膨張）する割合を、温度当たりで示したものである。熱膨張係数（ねつぼうちょうけいすう）とも呼ばれる。温度の逆数の次元を持ち、単位は毎ケルビン（記号: 1/K）である。

解説

温度の変化に伴って、物体の寸法は変形する。温度変化 ΔT に伴う物体のひずみ ε を

ε = α ΔT

で表わした時の係数 α を熱膨張係数と呼ぶ。ひずみが垂直ひずみ ε_l = Δl/l₀ である場合は

\alpha _{l}={\frac {1}{l}}{\frac {dl}{dT}}

となり、線膨張係数（線膨張率）と言う。ひずみが体積ひずみ ε_V = ΔV/V₀ である場合は

\alpha _{V}={\frac {1}{V}}{\frac {dV}{dT}}

となり、体膨張係数（体積膨張率）と言う。物体が等方的である場合には、二つの熱膨張係数の間には α_V ≒ 3α_l の関係がある。この定義における温度 T は、熱力学温度と、それを定数だけずらしたセルシウス温度やファーレンハイト温度の何れでも同じである。

一般に熱膨張係数は温度に依存して変化するが、殆どの固体や液体では通常の温度範囲で温度に依らずほぼ一定とみなすことができる。このとき、基準とする温度から ΔT だけ変化したときの物体の長さや体積は

l = l₀ (1 α_l ΔT )

V = V₀ (1 α_V ΔT )

と表わされる。ここで l₀, V₀ はそれぞれ基準とする温度における物体の長さと体積である。

熱膨張係数は原子間の結合の強さで決まる物性量であり、材料の融点と相関がある。

ある温度で体積変化を伴う相転移を起こす性質を利用して、使用温度領域で、線膨張が小さくなっている合金（アンバーまたはインバー合金）もある。

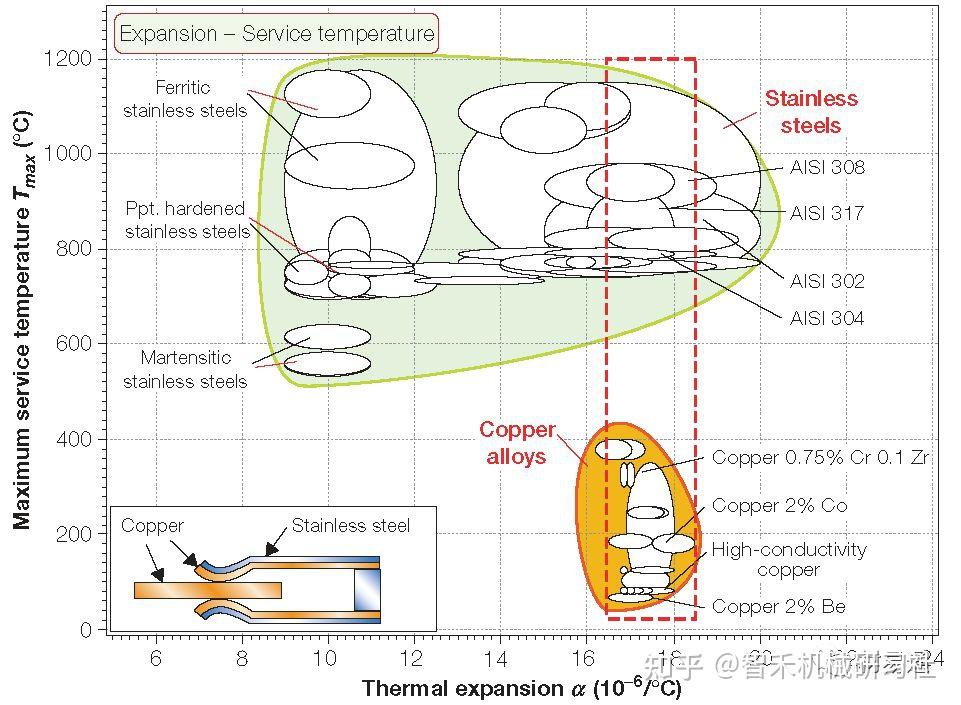
なお、熱膨張率の異なる材料を組合せて使う場合や、一様な材料でも急な熱勾配が生じた場合、熱膨張の違いから熱応力が生じる。この熱応力により、材料にクラックなどが入って壊れることがあり、様々なものの故障原因のひとつとなっている。

プルトニウムやタングステン酸ジルコニウムなどの一部の物質は、温度の上昇により収縮するという負の熱膨張を起こす。身近なところでは、水が0 ℃から3.98 ℃までの範囲で負膨張を起こす。近年では、理化学研究所が2005年に、マンガン窒化物をベースとした負膨張率の高い新素材の開発に成功している。

線膨張率と体積膨張率の関係

物体の体積 V と長さ l は無次元の係数 k を用いて V = k l³ で関係付けられる。物体が相似に変形する場合は k を定数として dV =3kl² dl となるので、体膨張係数と線膨張係数は

\alpha _{V}={\frac {1}{V}}{\frac {dV}{dT}}={\frac {3kl^{2}}{kl^{3}}}{\frac {dl}{dT}}={\frac {3}{l}}{\frac {dl}{dT}}=3\alpha _{l}

で関係付けられる。つまり体膨張係数 α_V は線膨張係数 α_l の3倍に等しい。

気体の体積膨張率

気体の場合は体積ではなく密度でその状態を表すことが多い。体積 V の気体の質量が m であるとき、密度は

\rho ={\frac {m}{V}}

である。熱膨張は気体の増減がない場合の体積変化なので、質量 m を定数として

d\rho =-{\frac {m\,dV}{V^{2}}}=-{\frac {\rho \,dV}{V}}

となる。体積膨張係数は

\alpha ={\frac {1}{V}}{\frac {dV}{dT}}=-{\frac {1}{\rho }}{\frac {d\rho }{dT}}

と表される。すなわち体膨張係数 α は密度の温度による変化率によっても表せる。

気体の体積は温度だけでなく圧力によっても大きく変化する。圧力を考慮する場合の熱膨張係数は圧力を一定に保った偏微分

\alpha ={\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{p}

で定義される。特に理想気体の場合は、理想気体の状態方程式を用いれば

\alpha ={\frac {1}{T}}

となる。ここで T は熱力学温度である。

主な物質の線膨張率

（10⁻⁶/K）

主な物質の体積膨張率

（10⁻⁴/K）

熱応力

温度変化による自由熱膨張（あるいは収縮）が拘束される場合に物体内に生じる応力を熱応力、ひずみを熱ひずみという。

線膨張率 α、ヤング率 E の棒が、その両端を固定され長さが変化しない状態で ΔT だけ温度変化したとき、その棒に生じる熱応力 σ_t と熱ひずみ ε_t は

{\begin{aligned}\sigma _{t}&=-\alpha E\Delta T,\\\epsilon _{t}&=-\alpha \Delta T\end{aligned}}

となる。

機械装置の起動時などのような過渡的な状態では、物体に急激な加熱または冷却が加わり一時的に大きな温度分布が生じることがある。このような場合に生じる熱応力を非定常熱応力、特に急速な非定常熱応力が生じる現象を熱衝撃という。熱衝撃の理論的な解析には、ビオ数が用いられる。

熱膨張を考慮した設計

殆どの固体の線膨張係数はごく小さく、通常の温度変化でのひずみは小さいが、その変形は物体の長さに比例するため、長大な物体では変形の影響が無視できない。

線路を敷く際にレールが夏に伸びることを前提として、レール同士の継ぎ目に隙間が設けられている。列車が「ガタンゴトン」と走行音を立てるのは、この継ぎ目を通過する際の音である（分岐器は別とする）。

電柱に架けられる送電線（架線）は夏は配線がたわんでも安全な高度を確保できるよう、冬は配線が縮れて破断しないよう、それぞれ念頭に設計される。

超音速で飛行する航空機は機体が断熱圧縮の影響で高温に晒されることから対策は必須である。特にマッハ3を優に超える高速で飛行するSR-71ブラックバードでは膨張が著しいことから、飛行中の機体状態を正常とすべく、部品同士に隙間が設けられている。これによって地上ではどうしても燃料類が漏れ出てしまう仕様となっていた。ただし引火点は極めて高く、マッチくらいで燃えることはない。オイルに至っては常温ではバター状になってしまう。